Wurzel-Rechtecke (Teil 2)
Dieser Artikel ist Teil einer Serie, die Bildkomposition unter Nutzung der Dynamischen Symmetrie und der Gestalttheorie behandelt. Teilweise werden Kenntnisse aus den anderen Artikeln vorausgesetzt. Am besten ist es, alle Artikel der Serie zu lesen.
In diesem Beitrag widmen wir uns der geometrischen Konstruktion der Wurzel-Rechtecke, den Beziehungen zwischen ihren Flächenverhältnissen und der Beziehung zum Satz des Pythagoras.
Wie schon im letzten Artikel erwähnt haben die Wurzel-Rechtecke eine große Bedeutung in der Kunstgeschichte. Es lohnt sich deshalb, sich mit ihnen näher zu beschäftigen.
Wie konstruiert man aber die Wurzel-Rechtecke? Ich stelle hier eine Methode
vor - die geometrische Konstruktion außerhalb eines Ausgangs-Quadrats. Es gibt auch noch
die Möglichkeit der geometrischen Konstruktion innerhalb eines Quadrats und natürlich
die rein numerische Berechnung. Auf Berechnungen gehe ich in einem späteren Artikel
noch einmal ein.
Bitte lesen Sie den Artikel bis zum Ende - eventuell überspringen Sie die Berechnungen.
Am Ende des Artikels gehe ich auf die geniale Denk-Leistung der alten Griechen ein, die
die Wurzel-Rechtecke so interessant macht.
Geometrische Konstruktion der Wurzel-Rechtecke
Die folgende Grafik veranschaulicht die geometrische Konstruktion:
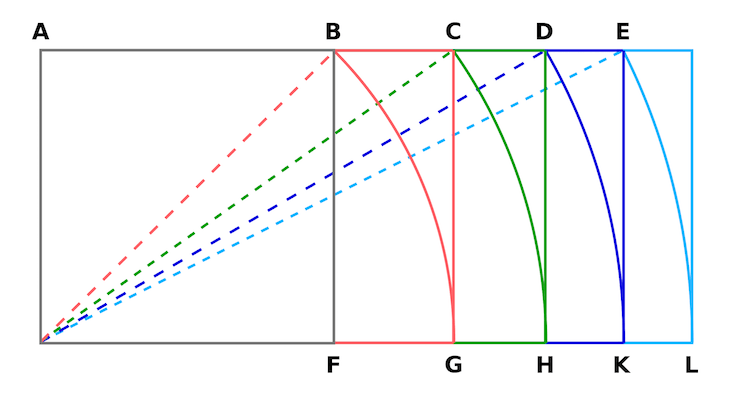
Ausgangspunkt ist das Quadrat zwischen den Punkten A und F. Die Diagonale
(rot gestrichelt) wird als Radius eines Kreises benutzt, dessen Schnittpunkt G
mit der Grundlinie die längere Seite des Wurzel-2-Rechtecks ergibt.
Das Wurzel-2-Rechteck liegt dann zwischen den Punkten A und G (rote Begrenzung).
Das Seitenverhältnis beträgt
Die Diagonale des Wurzel-2-Rechtecks (grün gestrichelt) wird wiederum als
Radius eines Kreises benutzt,
dessen Schnittpunkt H mit der Grundlinie die längere Seite des
Wurzel-3-Rechtecks ergibt. Dieses Rechteck liegt zwischen den Punkten A und
H (grün begrenzt).
Das Seitenverhältnis
beträgt hier
Und weiter:
Die Diagonale des Wurzel-3-Rechtecks (blau gestrichelt) wird wiederum als
Radius eines Kreises benutzt,
dessen Schnittpunkt K mit der Grundlinie die längere Seite des
Wurzel-4-Rechtecks ergibt. Dieses Rechteck liegt zwischen den Punkten A und
K (blau begrenzt).
Das Seitenverhältnis beträgt hier
Und weiter:
Die Diagonale des Wurzel-4-Rechtecks (hellblau gestrichelt) wird wiederum als
Radius eines Kreises benutzt,
dessen Schnittpunkt L mit der Grundlinie die längere Seite des
Wurzel-5-Rechtecks ergibt. Dieses Rechteck liegt zwischen den Punkten A und
L (blau begrenzt).
Das Seitenverhältnis beträgt
hier
Der Ausgangspunkt für die Konstruktion der Wurzel-Rechtecke ist immer das Quadrat.
Jedes Wurzel-Rechteck ist mit dem Quadrat sozusagen “verwandt”. Die Wurzel-Rechtecke
bilden eine Familie oder um
es etwas wissenschaftlicher auszudrücken - sie bilden ein System von Rechtecken.
Da diese Rechtecke zudem noch die besondere Eigenschaft haben, sich ganzzahlig in
ähnliche (mit gleichem Seitenverhältnis) kleinere Rechtecke aufteilen zu lassen
(siehe Wurzel-Rechtecke (Teil 1) und der nächste Artikel
Themen von Wurzel-Rechtecken), haben
die Wurzel-Rechtecke im Rahmen der Dynamischen Symmetrie die größte Bedeutung. Wie
früher schon erwähnt, kann
die Dynamische Symmetrie in jedem Rechteck angewendet werden, ihre beste Wirkung
entfaltet sie aber im Rahmen des Systems der Wurzel-Rechtecke.
Teil des Systems sind noch zwei andere Rechtecke, die mit dem Goldenen Schnitt zu tun
haben, diese werden aber in einem späteren Artikel behandelt.
Wegen dieser beiden “Familienmitglieder” spricht Myron Barnstone
übrigens bezüglich der Dynamischen Symmetrie (nicht ganz korrekt) vom “Golden Section System of Design” -
in Deutsch “Das Design-System des Goldenen Schnitts”. Um es klar zu sagen: Wurzel-Rechtecke
haben nichts mit dem Goldenen Schnitt zu tun. Deswegen ist diese Bezeichnung irreführend.
Warum ergeben sich hier jeweils Seitenverhältnisse von
Gehen Sie einmal gedanklich zurück in Ihre Schulzeit und erinnern Sie sich an den Satz des Pythagoras.
Sind a, b und c die Seitenlängen eines rechtwinkligen Dreiecks, wobei a und b
die Längen der Katheten und c die Länge der Hypotenuse ist, so gilt
Da die Diagonale eines Rechtecks (die wir hier zur Konstruktion benutzt haben) immer ein rechtwinkliges Dreieck innerhalb eines Rechtecks erzeugt, können wir den Satz des Pythagoras anwenden.
Das Beispiel für die Konstruktion des Wurzel-2-Rechtecks: Wenn wir von einem
Quadrat mit der Kantenlänge a ausgehen (mit b=a), dann ist die Länge der Diagonale
Setzen wir b für die weiteren Betrachtungen b immer auf den Wert 1 (unabhängig von
einer Maßeinheit) dann erhalten wir:
Die Rechnung für das Wurzel-3-Rechteck: a hat den Wert
Dann ergibt sich
Und noch die Rechnung für das Wurzel-5-Rechteck: a hat den Wert
Flächenverhältnisse der Wurzel-Rechtecke
Kommen wir nun zu einem für das Verständnis antiker Kunst und antiker Bauwerke wichtigen Aspekt der Wurzel-Rechtecke.
Stellen wir uns einmal die Frage warum sich jemand so “krumme” Seitenverhältnisse einfallen lassen sollte. Viele der Seiten-Verhältnisse lassen sich ja nicht einmal vernünftig als Dezimalzahl darstellen, da sie irrationale Zahlen sind.
Wenn Sie meinen letzten Artikel zum Thema
Wurzel-Rechtecke aufmerksam gelesen haben, können Sie sich vielleicht schon eine
Antwort vorstellen. Dort hatte ich erwähnt, dass die “altgriechische” oder “Dynamische”
Symmetrie Ähnlichkeiten und Wiederholungen meint und nicht im heutigen Wortsinn
verstanden wurde. Und ich hatte gezeigt, dass sich Wurzel-Rechtecke in mehrere Rechtecke
mit dem gleichen Seitenverhältnis teilen lassen.
Dabei fiel auch der Begriff
Umkehrung (siehe Artikel zu Umkehrungen).
Hier kommen wir zum Entscheidenden: Die Griechen haben nicht Seiten- (oder Längen-)
Verhältnisse für ihre Designs betrachtet. Nein - ihnen ging es immer um Flächen!
Das ist eine fundamentale Erkenntnis, die man erst einmal verinnerlichen muß. Deswegen will ich hier darstellen, wie einfach die Wurzel-Rechtecke im Grunde genommen zu verstehen sind.
Gehen wir wieder vom Satz des Pythagoras aus.
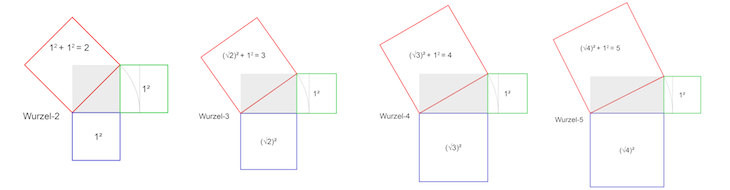
Die grafische Darstellung für den Satz des Pythagoras am Beispiel des Wurzel-2-Rechtecks sehen Sie hier:
Ausgangspunkt ist das graue Quadrat. Die farbigen Quadrate zeigen die Flächen,
die durch den Satz des Pythagoras gebildet werden. Das blaue Quadrat zeigt
Geht man wieder von einem Quadrat mit der Seitenlänge 1 aus, dann ergeben sich die
Flächeninhalte in den Beschriftungen. Ausgerechnet haben das blaue und das grüne
Quadrat jeweils die Fläche 1 und das rote Quadrat die Fläche 2.
Die Flächenverhältnisse sind also sehr viel einfacher als die Längenverhältnisse.
Sehen wir uns die Flächenverhältnisse für das Wurzel-3-Rechteck an.
Ausgangspunkt ist das graue Wurzel-2-Rechteck. Die Flächen sind 1 für das grüne Quadrat, 2 für das blaue und 3 für das rote Quadrat. Einfach, oder?
Und weiter für das Wurzel-4-Rechteck:
Ausgangspunkt ist das graue Wurzel-3-Rechteck. die Flächen sind 1 für das grüne Quadrat, 3 für das blaue und 4 für das rote Quadrat.
Um schliesslich das Wurzel-5-Rechteck:
Ausgangspunkt ist das graue Wurzel-4-Rechteck. die Flächen sind 1 für das grüne Quadrat, 4 für das blaue und 5 für das rote Quadrat.
Noch einmal Umkehrungen
Wie schon einige Male erwähnt, sind Rechteck-Umkehrungen ähnlich zu ihren Ursprungsrechtecken. Damit werden sie zu einem zentralen Instrument der Dynamischen Symmetrie. Interessant ist, dass vielen heutigen Künstlern zwar die Diagonale bekannt und auch “irgendwie wichtig” ist, aber die Umkehrung der Diagonalen ist laut Jay Hambidge nahezu unbekannt.
Umkehrungen von Rechtecken wurden und werden in der Architektur und Malerei zur harmonischen Aufteilung von Flächen verwendet. In einem weiteren Artikel werde ich darauf noch eingehen, wenn ich die Aufteilung und Zusammensetzung von Rechtecken behandle.
Im nächsten Artikel geht es aber erst einmal um Themen von Wurzel-Rechtecken. Schauen Sie wieder rein!




