Umkehrungen von Rechtecken und Diagonalen
Dieser Artikel ist Teil einer Serie, die Bildkomposition unter Nutzung der Dynamischen Symmetrie und der Gestalt-Theorie behandelt. Teilweise werden Kenntnisse aus den anderen Artikeln vorausgesetzt. Am besten ist es, alle Artikel der Serie zu lesen.

In den beiden letzten Artikeln zu Dynamischer Symmetrie (Bildkomposition mit Dynamischer Symmetrie und Gestalttheorie und Das Grundgerüst des Rechtecks in der Dynamischen Symmetrie) bin ich auf das Rechteck und sein Grundgerüst eingegangen.
Grundsätzlich kann man zu jedem Rechteck ein Grundgerüst wie im letzten Beitrag beschrieben erzeugen. Es gibt jedoch auch Rechtecke mit besonderen Eigenschaften. Das offensichtlichste Beispiel ist das Quadrat, bei dem alle Außenkanten gleich lang sind.
Zusätzlich gibt es so genannte Wurzel-Rechtecke, deren Außenkanten in einem Verhältnis stehen, das einem Wurzel-Ausdruck entspricht. Zum Beispiel kann die kurze Seite des Rechtecks die Länge “1” haben, und die lange Seite die Länge “Wurzel aus drei”. Das wäre dann ein Wurzel-3-Rechteck. Eine Eigenschaft dieser Seitenverhältnisse ist, dass sich diese oft nicht als Bruch darstellen lassen, da es sich um irrationale Zahlen handelt. Dazu wird es später einen weiteren Artikel geben.
Bevor man die Besonderheiten und das gestalterische Potenzial von Wurzel-Rechtecken verstehen kann, muss man ein anderes Prinzip verstehen: das der Umkehrung von Rechtecken und Diagonalen.
Wie in den vorangegangenen Artikeln schon erwähnt hat die Dynamische Symmetrie nichts mit unserem heutigen Verständnis von Symmetrie zu tun. Im alten Griechenland war Symmetrie ein Begriff für die Ähnlichkeit und Wiederholung. Im Zusammenhang damit stehen die Begriffe Proportion und Ratio (Verhältnis). Letztendlich dreht sich in der Dynamischen Symmetrie alles um diese zentralen Begriffe.
Was ist eine Umkehrung eines Rechtecks? Wenn Sie sich das Titelbild ansehen, können Sie die Definition vielleicht schon erkennen - hier sehen sie ein Wurzel-9-Rechteck mit seiner Umkehrung.
Definition:
Die Umkehrung eines Rechtecks hat das gleiche Seitenverhältnis wie das
Ursprungsrechteck. Die Lange Seite der Umkehrung ist hierbei genau so
lang wie die kurze Seite des originalen Rechtecks.
Da die Umkehrung (Punkte 2, 3, 6, 5) eine gleich lange Seite wie das Original-Rechteck (Punkte 1, 2, 3, 4) hat, kann man die kurze Seite des Original-Rechtecks gleich als lange Seite der Umkehrung (Punkte 2 und 3) benutzen und die Umkehrung am Rand in das Ursprungsrechteck einsetzen (hier ein Beispiel für das 1,5-Rechteck):
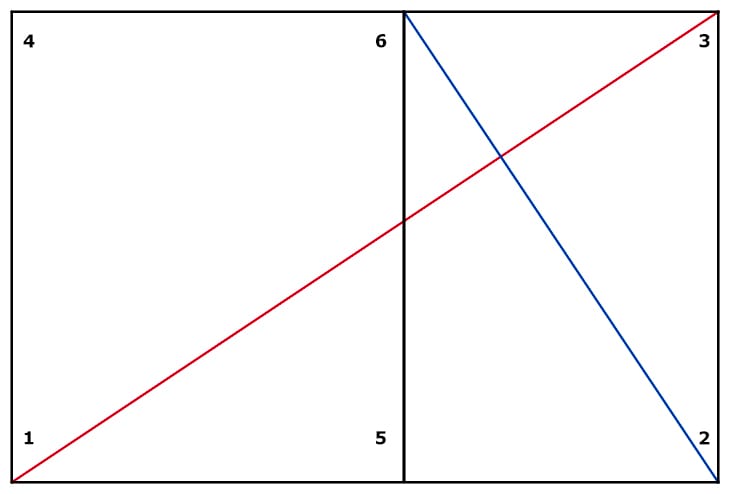
Geometrisch läßt sich die Umkehrung eines Rechtecks konstruieren, indem man die Diagonale einzeichnet (rot, Punkte 1 und 3) und dann zu dieser ihre Umkehrung (90° gedreht - blau dargestellt, Punkte 2 und 6). Die Diagonalen-Umkehrung schneidet den Rand an dem Punkt, der die Begrenzung der Umkehrung des Rechtecks markiert (Punkt 6).
Hier ist schon eine wichtige Eigenschaft der Dynamischen Symmetrie zu sehen - die Diagonale spielt eine Rolle und vor allem ihre Umkehrung. Diese blaue Linie ist es, die laut Jay Hambidge vielen aktuellen Künstlern (und Fotografen) unbekannt ist. Sie ist aber entscheidend für die harmonische Aufteilung von Flächen.
Und wir können noch etwas feststellen: Der Satz, dass ein Rechteck zu jedem anderen Rechteck ähnlich ist, das die gleiche Diagonale besitzt (siehe letzter Artikel) ist erweiterbar. Wie im Beispielbild leicht zu sehen ist, ist das Rechteck dann auch ähnlich zu den Umkehrungen - also zu allen Rechtecken, die eine “umgekehrte” Diagonale (Reziproke) besitzen. Diese Feststellung wird in weiteren Artikeln noch Bedeutung erlangen.
In der Folge werden noch weitere Artikel zu Dynamischer Symmetrie und auch zu Gestalt-Theorie auf diesem Blog erscheinen. Falls Sie Interesse daran gefunden haben, schauen Sie wieder mal rein.