Das Grundgerüst des Rechtecks in der Dynamischen Symmetrie
Dieser Artikel ist Teil einer Serie, die Bildkomposition unter Nutzung der Dynamischen Symmetrie und der Gestalt-Theorie behandelt. Teilweise werden Kenntnisse aus den anderen Artikeln vorausgesetzt. Am besten ist es, alle Artikel der Serie zu lesen.

Im letzten Beitrag habe ich einen kurzen Überblick zu Dynamischer Symmetrie gegeben. Hierbei war mehrfach ein Netz aus Linien dargestellt, das über den gegebenen Rahmen bzw. das vorhandene (rechteckige) Bild gelegt wurde.
Wie erstellt man das oben genannte Grundgerüst?
Das Grundgerüst des Rechtecks in der Dynamischen Symmetrie besteht aus den folgenden Bestandteilen:
- die Diagonalen
- die Umkehrungen der Diagonalen (Englisch: reciprocals)
- eventuell vertikale und horizontale Linien, die durch bestimmte Schnittpunkte verlaufen
Der Konstruktionsverlauf ist für jedes Rechteck gleich - beim Quadrat fallen allerdings die Umkehrungen der Diagonalen mit den Diagonalen zusammen.
Ausgangspunkt ist unser leerer “Rahmen” bzw. das Rechteck.

Diagonalen
Wir starten mit den Diagonalen. Der erste Schritt ist, die “positive” (baroque) Diagonale zu zeichnen:
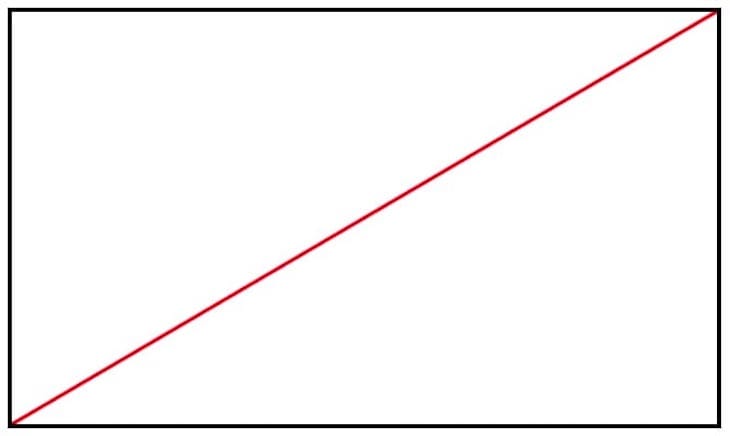
Die zweite Diagonale (hier blau dargestellt) ist die “negative” Diagonale - englisch “sinister diagonal”:
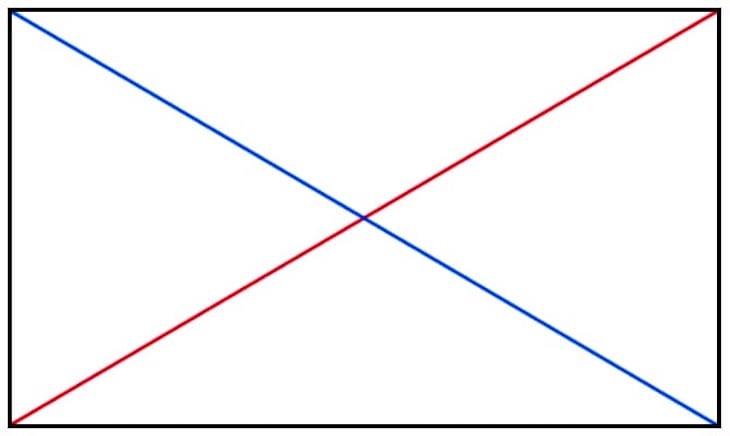
Umkehrungen der Diagonalen
Nun folgen die Umkehrungen der Diagonalen. Die Umkehrungen stehen in einem 90-Grad-Winkel zu den Diagonalen. Im Englischen heißen sie “reciprocals”. Gezeichnet werden die Umkehrungen ausgehend von einer Ecke des Rechtecks.
Zunächst zeichnen wir die Umkehrungen der positiven Diagonale - hier orange dargestellt. Sie beginnen jeweils in der linken oberen Ecke und in der rechten unteren Ecke.
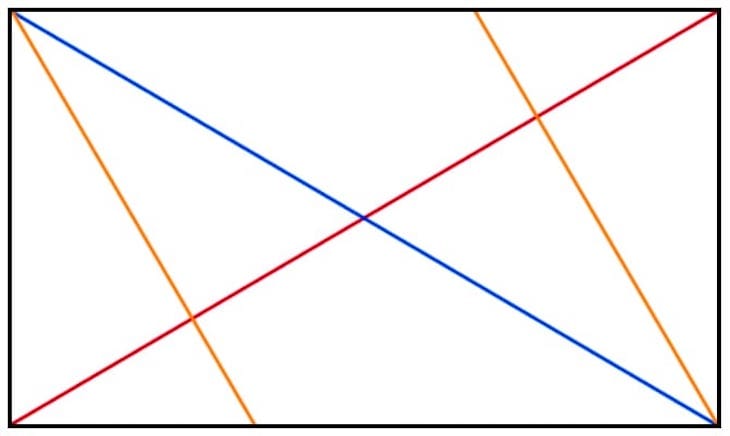
Nun folgen die beiden Umkehrungen der negativen Diagonale. Diese beginnen in den beiden verbleibenden Ecken (links unten und rechts oben). Die Umkehrungen sind hier grün dargestellt:
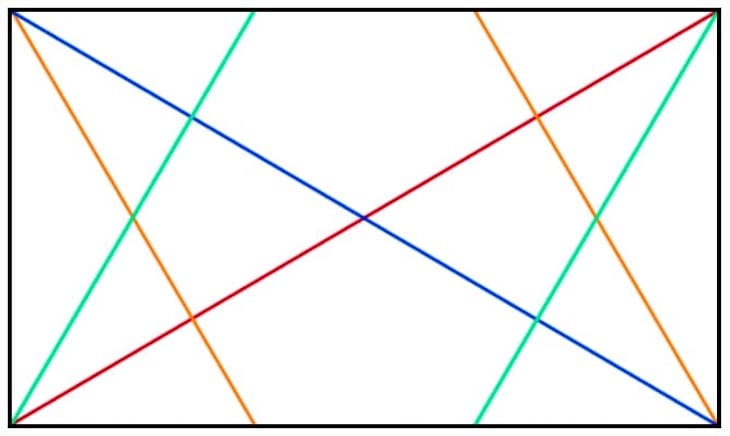
Schon an diesem Punkt kann man erkennen, wie vielfältig die Gestaltungsmöglichkeiten für ein Bild werden, wenn man die Dynamische Symmetrie einsetzt. Wir haben eine harmonische Flächenaufteilung zur Verfügung und insgesamt vier Richtungen, in denen Linien in unserem Bild verlaufen können. Diese Linien müssen nicht direkt mit dem Gitter zusammenfallen - auch Parallelen dazu passen in unser Grundgerüst.
Vertikale und Horizontale
Vertikale und horizontale Linien gehören auch zu unserer Welt und finden sich so ziemlich in jedem Bild wieder. Kommen wir zunächst zu den vertikalen Linien, an denen man Bildbestandteile ausrichten kann.
Die vertikalen Linien, die zwischen den Schnittpunkten der Umkehrungen mit dem Rand des Rechtecks verlaufen, sind die gebräuchlichsten: hier in Grau dargestellt:
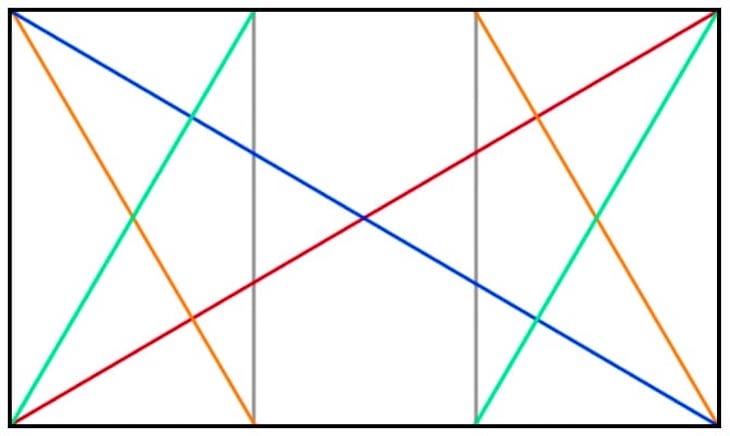
Ein Vorteil dieser Senkrechten ist, dass sie an den Rändern
des Rechtecks zwei Rechtecke erzeugen, die die gleichen
Seitenverhältnisse aufweisen wie unser gesamtes Rechteck.
Damit sind wir wieder beim Kernpunkt der Dynamischen Symmetrie: der Ähnlichkeit.
Die beiden Rechtecke sind untereinander gleich und zum Gesamt-Rechteck
ähnlich. Das liegt einfach daran, dass sie um 90 Grad gedreht sind und
ihre Diagonalen die Umkehrungen der Hauptdiagonalen des Gesamt-Rechtecks sind.
Jedes Rechteck, dessen Diagonale den gleichen Winkel oder einen um
90 Grad versetzten Winkel wie ein anderes Rechteck hat, ist diesem
Rechteck ähnlich oder anders gesagt: es hat die gleichen Seitenverhältnisse.
Kommen wir zu den horizontalen Linien. Die Kreuzungspunkte der Diagonalen mit ihren Umkehrungen sind die auffälligste Stelle, wo man Horizontalen ziehen kann:
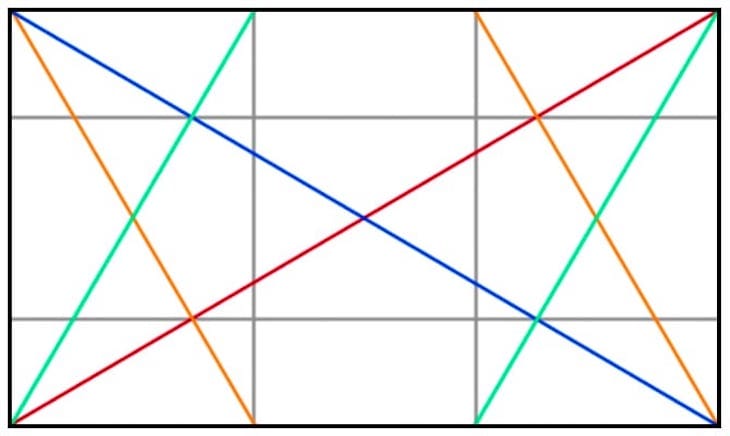
Was kann man damit anfangen? Zum Beispiel kann man an diesen Linien die Übergänge von Vordergrund zu Hintergrund oder den Horizont oder auch die Blickrichtung eines Fotomodells ausrichten.
Natürlich sind diese vertikalen und horizontalen Linien nicht die einzigen Möglichkeiten - man kann auch ihre Umkehrungen wählen.
Die vertikalen Linien würden dann durch die Kreuzungspunkte der Diagonalen mit ihren Umkehrungen verlaufen, wie hier dargestellt:
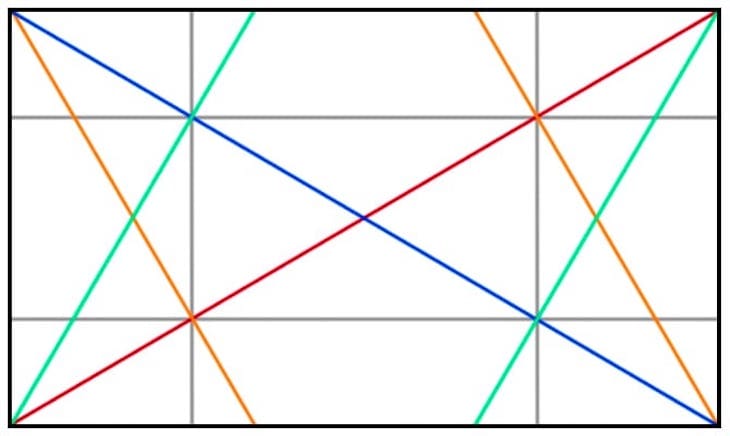
Bei den Horizontalen würden diese durch die Schnittpunkte der Diagonalen mit den erstgenannten Vertikalen verlaufen:
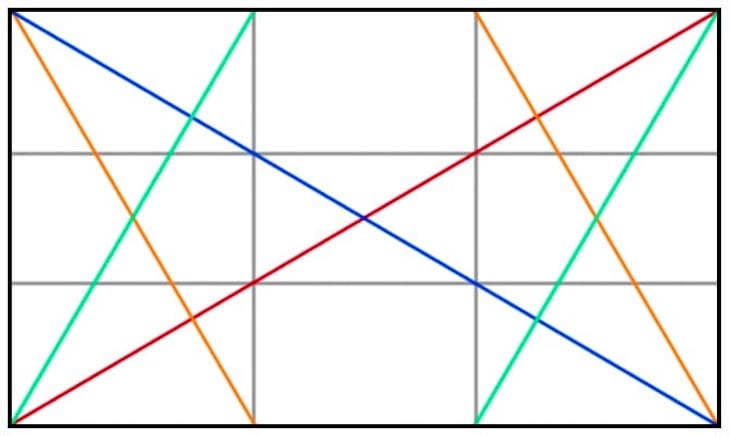
Erkennen Sie, warum ich die beiden letzten Varianten Umkehrungen genannt habe? Falls nicht, schauen Sie sich an, wie die Linien dann durch die beiden inneren (gedrehten) Rechtecke verlaufen.
Mittellinien
Natürlich sind auch die Mittellinien interessant - sie spielen unter anderem für die Balance des Bildes eine Rolle, auch wenn sie nicht als sichtbare Linie im Bild auftauchen. In der Darstellung können Sie sie als gepunktete Linie sehen:
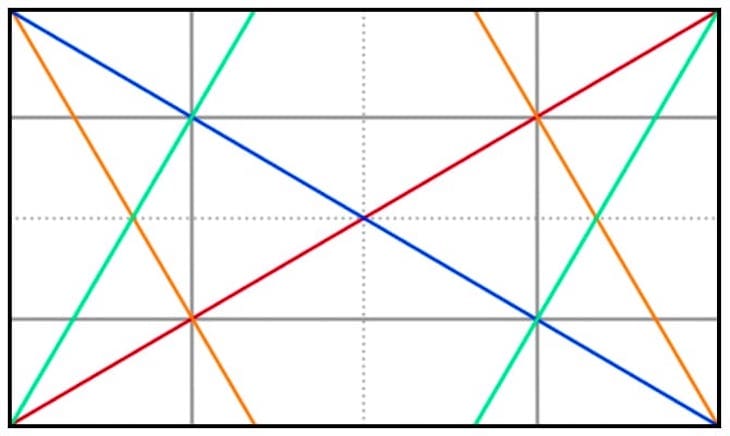
Gesamtbild
Hier sehen Sie das Grundgerüst des Rechtecks in der Dynamischen Symmetrie komplett mit allen Möglichkeiten:
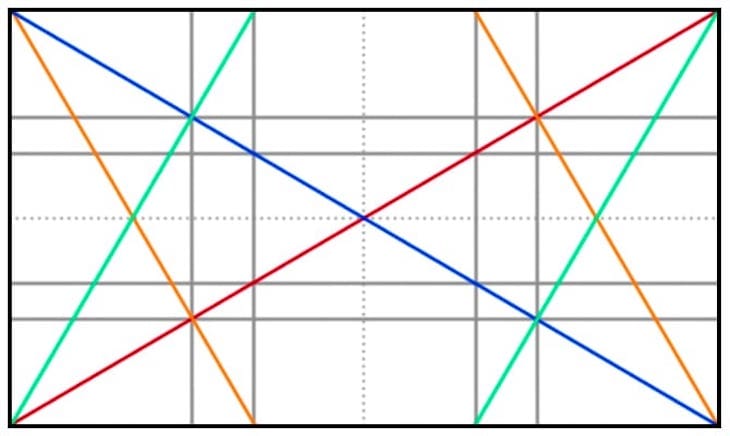
Eine Unmenge an Gestaltungsmöglichkeiten - alle basierend auf einem einfachen Prinzip - der Ähnlichkeit!
Machen Sie sich einmal die Mühe und versuchen Sie zu zählen, wie viele Rechtecke sich in dieser Darstellung verbergen, die dem Gesamt-Rechteck ähnlich sind! Und jedes dieser Teil-Rechtecke kann wiederum nach den gleichen Prinzipien unterteilt werden.
Aber: noch einmal der Hinweis aus dem ersten Artikel: Allein durch die Anordnung der Bildelemente in einem solchen Grundgerüst erreicht man noch kein gutes Bild. Das gilt hier ebenso wie bei der Drittel-Regel. Das Grundgerüst erleichtert es dem Künstler aber, seine Bildelemente so anzuordnen, dass ein ausgewogener und harmonischer Bildeindruck entsteht.
Und jetzt die Warnung:
Das Grundgerüst ist nur dann harmonisch, wenn die Diagonalen und ihre Umkehrungen in einem rechten Winkel zueinander stehen:
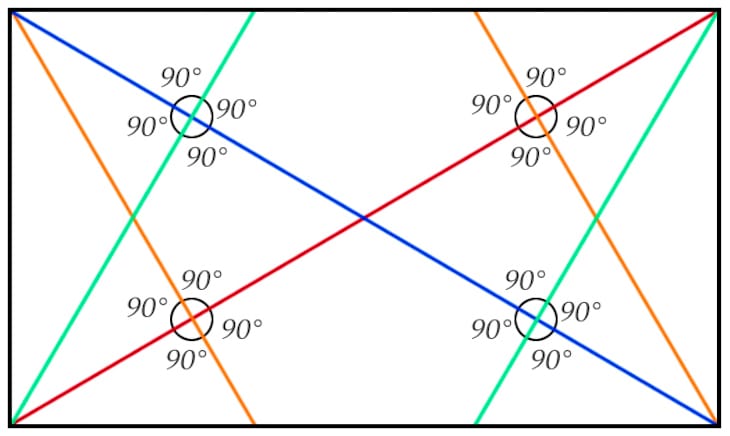
Das heisst: Ein Bild, das mit Dynamischer Symmetrie gestaltet wurde,
kann nicht in seinen Seitenverhältnissen geändert werden. Man kann
auch nicht an einer Seite etwas abschneiden, um das Bild für irgendetwas
passend zu machen - damit zerstört man das Grundgerüst, da sich die
Seitenverhältnisse des Rahmens ändern. Die Seitenverhältnisse des
Rahmens legen das Grundgerüst fest.
Auch das Strecken oder Stauchen eines Bildes ist nicht möglich, da
sich auch dadurch das Grundgerüst ändern würde. Wie im folgenden Bild
zu sehen ist, würde eine vertikale Stauchung des Bildes die rechten
Winkel des Grundgerüstes verändern und damit die Harmonie des Bildes:
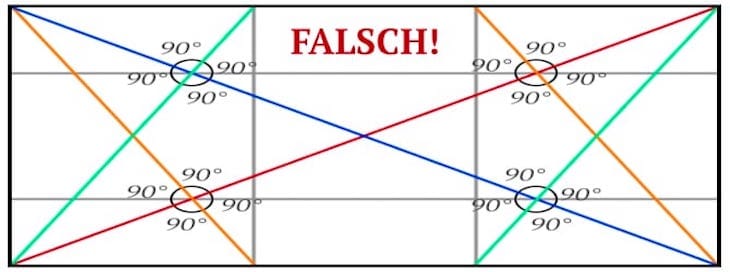
In der Folge werden noch weitere Artikel zu Dynamischer Symmetrie und auch zu Gestalt-Theorie auf diesem Blog erscheinen. Falls Sie Interesse daran gefunden haben, schauen Sie wieder mal rein.