Fotografie Blog

Dieser Artikel ist Teil einer Serie, die Bildkomposition unter Nutzung der Dynamischen Symmetrie und der Gestalttheorie behandelt. Teilweise werden Kenntnisse aus den anderen Artikeln vorausgesetzt. Am besten ist es, alle Artikel der Serie zu lesen.

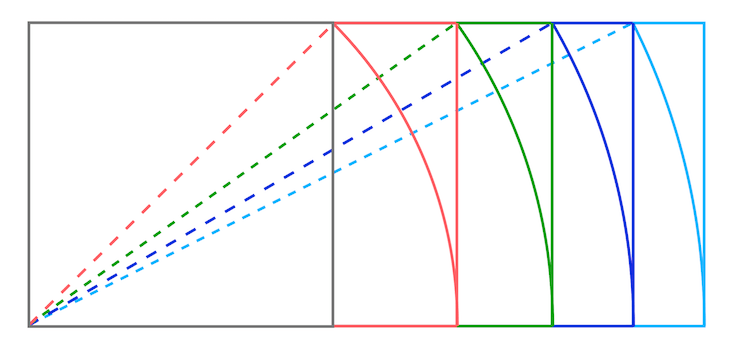
In diesem Beitrag widmen wir uns den Wurzel-Rechtecken. Der Name ist im Deutschen etwas sperrig - im Englischen heissen diese “Root-Rectangles”. Das bedeutet zwar das Gleiche, ist aber etwas leichter auszusprechen.

Auch wenn dieser Artikel sehr theoretisch erscheint, haben Wurzel-Rechtecke eine große Bedeutung und auch eine lange Historie in der Kunst. Zu jedem der Wurzel-Rechtecke gibt es spezielle Anwendungsgebiete - zum Beispiel das Wurzel-2-Rechteck wurde oft als Format für Portraits verwendet und das Wurzel-5-Rechteck findet in Gemälden mit weiten Landschaften oder dem Meer eine häufige Anwendung.

Für das Verständnis des Artikels ist es von Vorteil, schon einmal die beiden Artikel “Das Grundgerüst des Rechtecks in der Dynamischen Symmetrie” und “Umkehrungen von Rechtecken und Diagonalen” gelesen zu haben. Dort werden einige Begriffe erklärt, die hier verwendet werden.

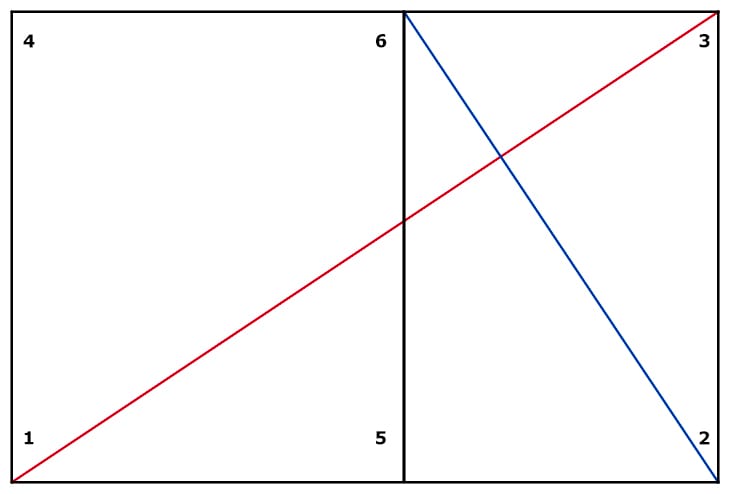
Erinnern wir uns daran, wie das Grundgerüst des Rechtecks in der Dynamischen Symmetrie aussieht: ausgehend von einer Diagonalen (zwischen den Punkten 1 und 3) wird ihre Umkehrung (von Punkt 2 zu Punkt 6) eingezeichnet. Der Schnittpunkt der Umkehrung der Diagonalen mit der Aussenkante des Rechtecks (Punkt 6) definiert wiederum ein Rechteck (zwischen den Punkten 6, 5, 2 und 3). Dieses Rechteck ist die Umkehrung des ursprünglichen Rechtecks (zwischen den Punkten 1, 2, 3 und 4).

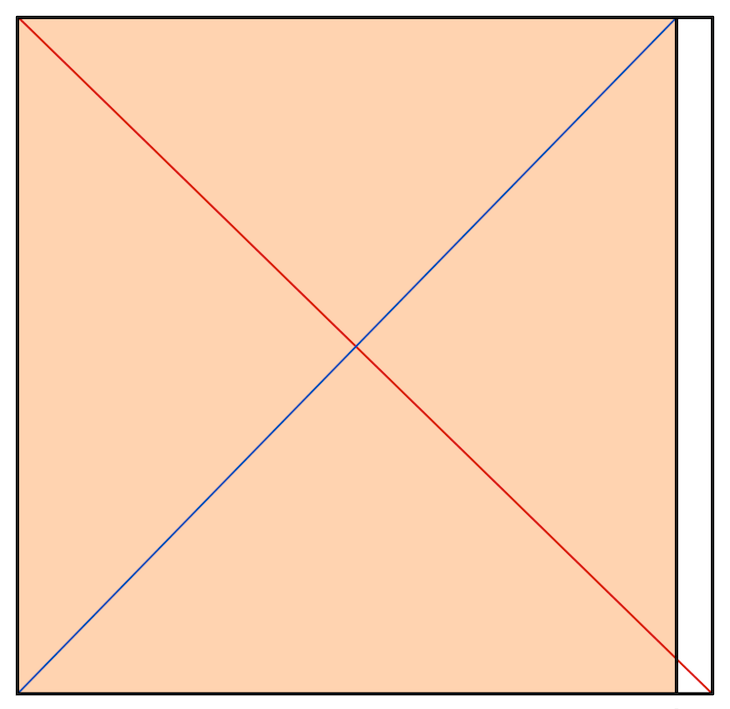
Bei einem Quadrat ist offensichtlich die Umkehrung auch wiederum ein Quadrat. Je langgestreckter das Rechteck wird (bzw. je größer sein Seitenverhältnis), desto langgestreckter wird auch seine Umkehrung. Das liegt daran, dass die Umkehrung eines Rechtecks das gleiche Seitenverhältnis aufweist wie das Ursprungsrechteck.

Schauen wir uns zunächst ein Rechteck an, das fast quadratisch ist. Lassen Sie sich nicht dadurch verwirren, dass hier für die Konstruktion der Umkehrung die negative Diagonale benutzt wurde. Das ist genauso möglich, wie die Benutzung der postitiven Diagonalen. Die farblich markierte Fläche ist die Umkehrung des Gesamt-Rechtecks.

Jetzt strecken wir das Rechteck etwas - in diesem Fall benutzen wir ein Seitenverhältnis von 1,5. Dieses Rechteck entspricht dem Seitenverhältnis von Fotos einer Kleinbildkamera:

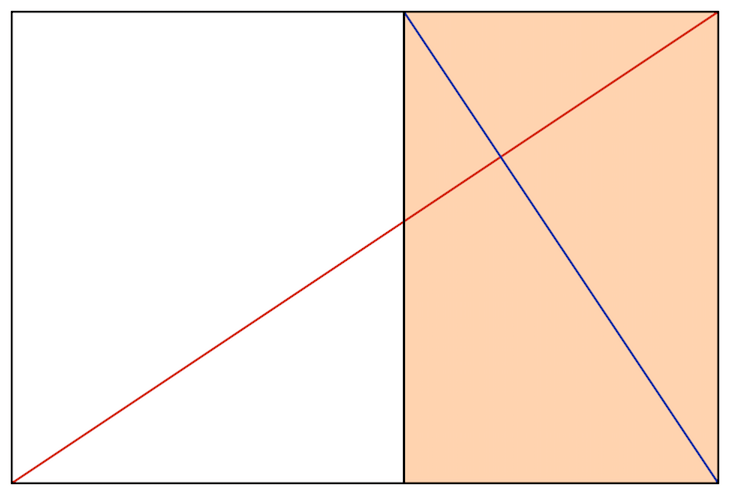
Es ist klar zu erkennen, wie sich das Seitenverhältnis der Umkehrung analog zum Seitenverhältnis des Gesamtrechtecks ändert. Schauen wir uns noch ein Extrem-Beispiel an - ein sehr schmales Rechteck bzw. eins mit einem großen Seitenverhältnis:

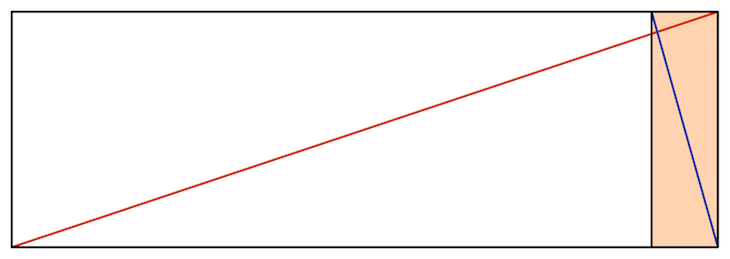
Wie schon in den vorherigen Beispielen entspricht das Seitenverhältnis der Umkehrung dem Seitenverhältnis des Gesamt-Rechtecks.

Ausgehend von dieser festen Beziehung der Seitenverhältnisse hat Jay Hambidge (siehe Einführungs-Artikel) folgende Überlegung angestellt:

Ändert man das Seitenverhältnis des Rechtecks schrittweise, so muss es Seitenverhältnisse geben, bei denen die Umkehrung des Rechtecks mehrfach in das Gesamt-Rechteck passen, so dass kein freier Bereich übrig bleibt.

Mathematisch ausgedrückt: Es muss Seitenverhältnisse geben, bei denen die lange Seite des Gesamtrechtecks ein ganzzahliges Vielfaches der kurzen Seite der Umkehrung ist. In der obigen Grafik (mit den Nummern) wäre also die Strecke zwischen den Punkten 1 und 2 ein ganzzahliges Vielfaches der Strecke zwischen den Punkten 5 und 2. Da die Grafik kein Wurzelrechteck darstellt ist dies dort natürlich nicht so.

Warum ist die ganzzahlige Aufteilung von Rechtecken interessant?

Erinnern wir uns daran, was die Griechen unter Symmetrie verstanden: Das, was wir heute als “Ähnlichkeit” bezeichnen.
Also eine Wiederholung von geometrischen Formen und Flächenverhältnissen in anderen Größen oder Anordnungen. Eine Aufteilung eines Rechtecks in mehrere kleinere Rechtecke mit dem gleichen Seitenverhältnis ist eine der offensichtlichsten Anwendungen für die “griechische” oder Dynamische Symmetrie.

Warum heißen die Rechtecke mit diesen speziellen Seitenverhältnissen Wurzel-Rechtecke?

Die Antwort hierauf ist einfach. Berechnet man die Seitenverhältnisse, bei denen sich eine ganzzahlige Aufteilung des Rechtecks in kleinere Rechtecke mit dem identischen Seitenverhältnis ergibt, dann erhält man jeweils die Wurzel aus der Anzahl der kleineren Rechtecke.

Beim Quadrat (Wurzel-1-Rechteck) ist die Aufteilung offensichtlich - man kann nur ein Teil-Rechteck erzeugen und das ist identisch mit dem Gesamt-Quadrat. Das Seitenverhältnis des Quadrats ist 1:$ sqrt(1) $, oder auch einfach 1:1.

Das Wurzel-2-Rechteck enthält zwei kleinere Rechtecke. Das Seitenverhältnis des Gesamt-Rechtecks und der Teil-Rechtecke beträgt $ sqrt(2) $:1 oder als Zahl angegeben ungefähr 1,414:1. Den genauen Wert kann man nicht als Dezimalzahl angeben, da es sich um eine irrationale Zahl handelt - diese haben unendlich viele Nachkommastellen.

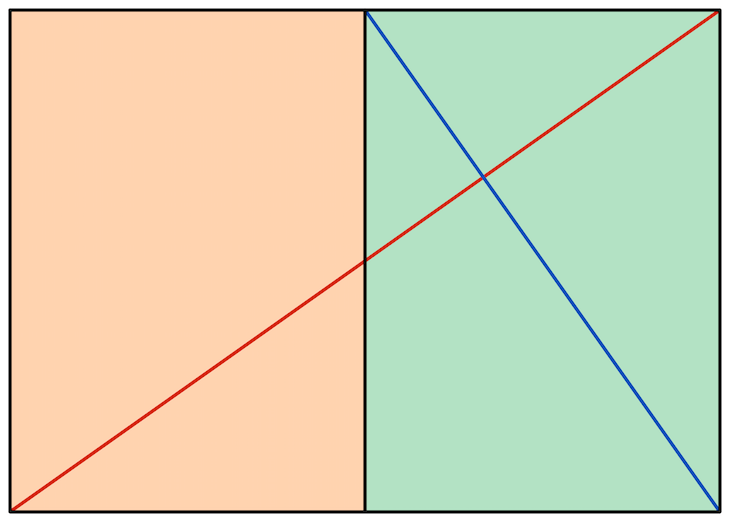
Das Wurzel-3-Rechteck enthält drei kleinere Rechtecke. Das Seitenverhältnis beträgt hier $ sqrt(3):1 $ oder als ungefähre Dezimalzahl angegeben 1,732:1.

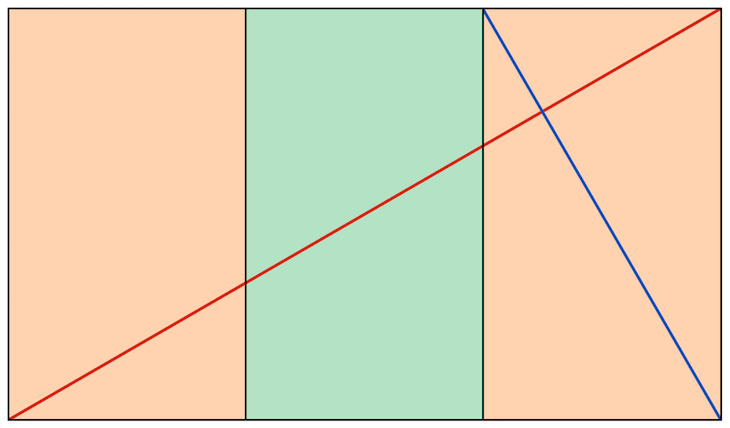
Das Wurzel-4-Rechteck enthält vier kleinere Rechtecke. Das Seitenverhältnis beträgt hier $ sqrt(4) $:1 oder als Dezimalzahl ausgedrückt 2:1.

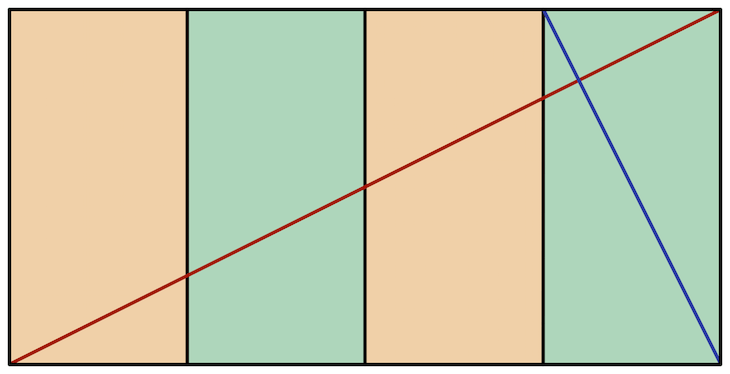
Das Wurzel-5-Rechteck enthält fünf kleinere Rechtecke. Das Seitenverhältnis beträgt hier $ sqrt(5) $:1 oder als Dezimalzahl ausgedrückt 2,236:1.

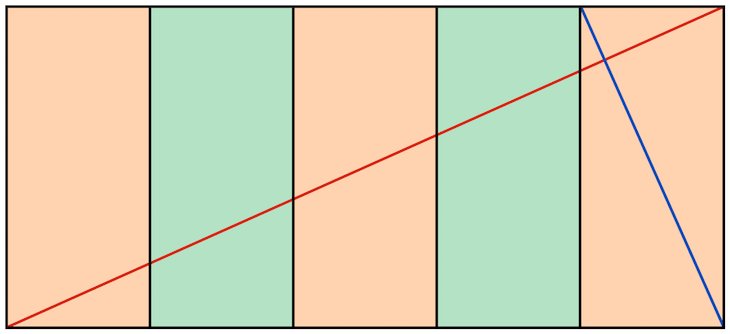
Natürlich gibt es auch noch weitere Wurzel-Rechtecke, wenn man das Seitenverhältnis weiter erhöht. In der Praxis sind aber nur die Rechtecke bis Wurzel-5 relevant. Breitere Formate werden in der Regel durch zusammengesetzte und überlagerte Wurzel-Rechtecke erzeugt.

Im nächsten Artikel wird es darum gehen, wie man die Wurzel-Rechtecke geometrisch konstruiert und wie man sie auch noch anders in kleinere Rechtecke aufteilen kann.

Falls Sie Interesse an Dynamischer Symmetrie gefunden haben, schauen Sie wieder mal rein.