Themen von Wurzel-Rechtecken
Beim Studium der Videos von Myron Barnstone und auch in einigen Artikeln von Tavis Leaf Glover wurden “Themen” von Wurzel-Rechtecken (und auch anderen Spezial-Rechtecken) erwähnt. Ein Thema ist dabei so zu verstehen, dass die Aufteilung des Rechtecks in eine bestimmte Anzahl von Teil-Rechtecken möglich ist bzw. durchgeführt wird.
Speziell zu den Wurzel-Rechtecken gab es die Aussage, dass zu Wurzel-n-Rechtecken (für den Fall dass n eine natürliche Zahl ist) jeweils die Themen n und n+1 gibt. Weil das geometrisch nicht einfach ersichtlich ist, habe ich diese Aussage mathematisch bewiesen.
Wenn im folgenden Beispiel (Wurzel-3-Rechteck) die Senkrechte ausgehend vom Schnittpunkt der Umkehrung der Diagonalen (blau) mit der Aussenkante des Rechtecks (Punkt A) gezogen wird, erzeugt man eine Umkehrung des Rechtecks, die die gleichen Seitenverhältnisse aufweist wie das Ursprungsrechteck (siehe Umkehrungen von Rechtecken und Diagonalen). Da es sich bei unserem Beispiel um ein Wurzel-3-Rechteck handelt, passen genau drei dieser Umkehrungen in das Gesamtrechteck. Im Bild sind diese verschieden farbig markiert:
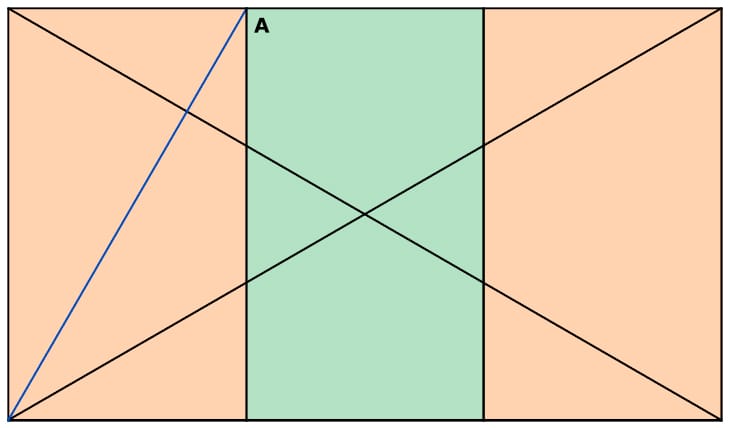
Sie sehen hier ein Wurzel-3-Rechteck zum Thema 3.
Nun sehen Sie sich ein Wurzel-3-Rechteck zum Thema 4 an. Die Senkrechte wird durch den Punkt B gezogen - die Kreuzung der Diagonalen mit ihrer Umkehrung. Das erzeugt ein Rechteck, das genau ein Viertel der Fläche des Gesamt-Rechtecks belegt. Die anderen drei Rechtecke sind ergänzt und farbig markiert:
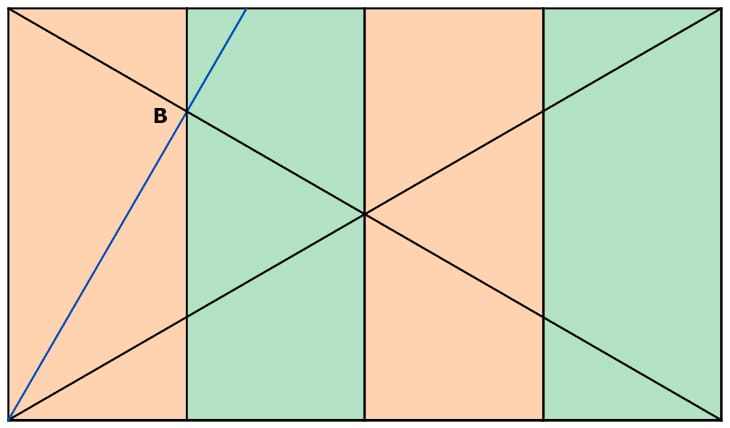
Nach dem gleichen Schema können Sie auch Wurzel-2-, Wurzel-4- und Wurzel-5-Rechtecke aufteilen, sogar mit Quadraten geht das, die ja Wurzel-1-Rechtecke sind.
Die folgenden Bilder zeigen die Aufteilung eines Wurzel-5-Rechtecks zum Thema 5 und zum Thema 6.
Thema 5:
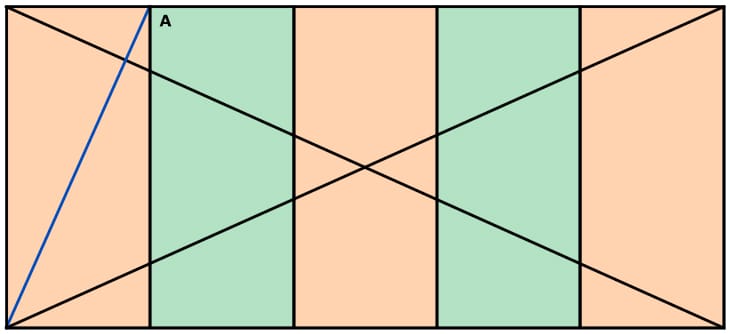
Thema 6:
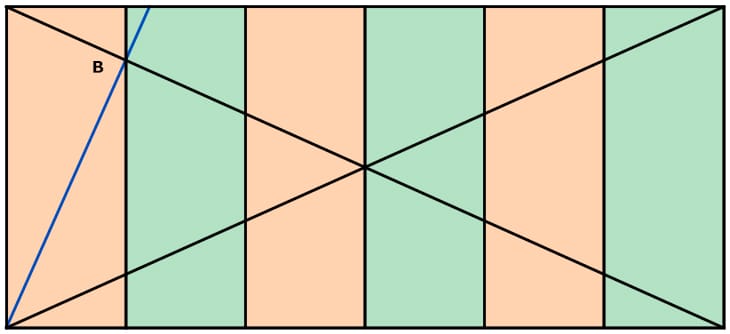
Die obigen Illustrationen sollten Ihnen eine Vorstellung davon geben, worum es in diesem Artikel geht. Lassen Sie uns mit den mathematischen Beweisen anfangen.
Das folgende Bild zeigt eine Illustration aller Variablen, die in den Berechnungen benutzt werden.
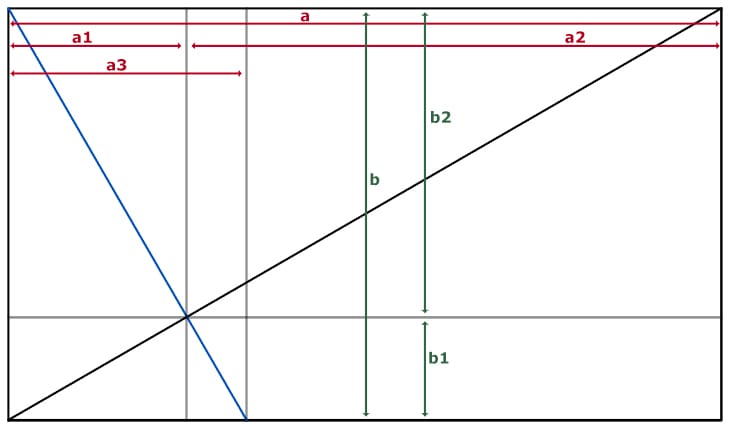
- a ist die längere Seite des Wurzel-n-Rechtecks
- a1 ist der Teil von a, der durch das n+1-Thema erzeugt wird, a2 ist der Rest von a in diesem Fall
- a3 ist der Teil von a, der durch das n-Thema erzeugt wird
- b ist die kurze Seite des Wurzel-n-Rechtecks
- b1 ist die “Höhe” des Kreuzungspunkts zwischen der Diagonalen und ihrer Umkehrung, b2 ist der Rest von b (b-b1)
- dargestellt sind ebenso die positive Diagonale (schwarz) und ihre Umkehrung (blau)
- die grauen Linien zeigen die Senkrechten des n- und des n+1-Themas und die Horizontale durch den Kreuzungspunkt zwischen der Diagonalen und ihrer Umkehrung
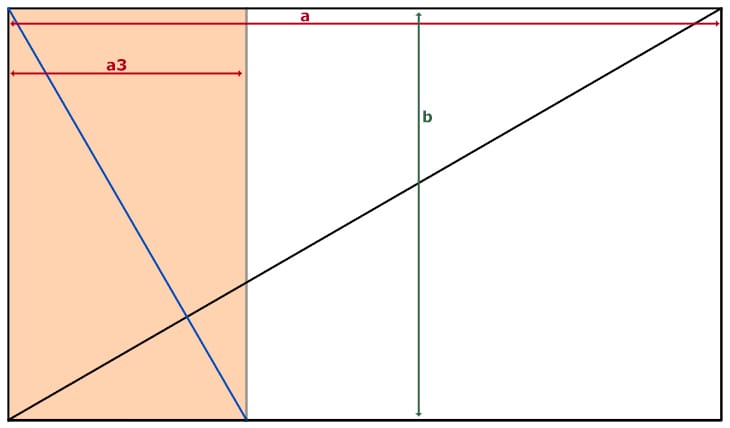
Beweis für das n-Thema
Ein Tipp: Lassen Sie sich nicht von den Formeln erschrecken. Sie sind einfach zu verstehen
und ich habe jeden einzelnen Schritt zu ihrer Umformung dargestellt.
Versuchen Sie es - ich denke Sie werden alles verstehen.
- Die Eigenschaft, die ein Wurzel-n-Rechteck definiert, ist das Seitenverhältnis
zwischen seiner langen und kurzen Seite.
Also gilt für ein Wurzel-n-Rechteck (wenn n eine natürliche Zahl ist) folgende Definition: $ a = b * sqrt(n) $ - Das farblich markierte Rechteck in der obigen Darstellung, das durch die Strecken
b und a3 geformt wird hat das gleiche Seitenverhältnis wie das “große”
Wurzel-n-Rechteck. Seine Diagonale ist 90 Grad versetzt zu der des großen Wurzel-n-Rechtecks.
Alle Rechtecke, die die gleiche Diagonale haben oder eine um 90 Grad versetzte Diagonale haben das gleiche Seitenverhältnis.
Ausgedrückt als Formel:
$ b = a3 * sqrt(n) $ - Unser Ausgangspunkt ist die Formel aus Schritt 1. Wir ersetzen in dieser Formel die Variable
b durch die Formel, die wir in Schritt 2 aufgeschrieben haben:
$ a = ( a3 * sqrt(n) ) * sqrt(n) $ - Anders zusammengefaßt sieht die Formel dann so aus:
$ a = a3 * ( sqrt(n) * sqrt(n) ) $ - Da die Multiplikation einer Quadratwurzel mit sich selbst als Ergebnis den Wert unter
der Wurzel ergibt, haben wir jetzt folgendes Ergebnis:
$ a = a3 * n $
Cool. Das ist exakt, was wir beweisen wollten. Jetzt wissen wir, dass in einem Wurzel-n-Rechteck genau n Rechtecke von der Größe der Umkehrung des Rechtecks enthalten sind.
Also: Jedes Wurzel-n-Rechteck kann in n gleich große Rechtecke geteilt werden, die auch jeweils wieder Wurzel-n-Rechtecke sind.
Beweis für das n+1-Thema
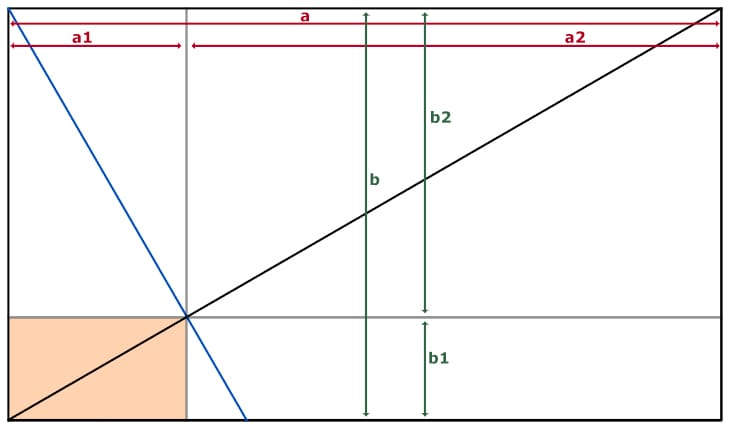
- Die Eigenschaft, die ein Wurzel-n-Rechteck definiert, ist das Seitenverhältnis
zwischen seiner langen und kurzen Seite.
Also gilt für ein Wurzel-n-Rechteck (wenn n eine natürliche Zahl ist) folgende Definition: $ a = b * sqrt(n) $ oder umgekehrt ausgedrückt: $ b = a / sqrt(n) $ - Wie oben beschrieben ist b die Summe aus b1 und b2:
$ b = b1 + b2 $ oder $ b2 = b - b1 $ - Das farblich markierte Rechteck, das durch die Strecken a1/b1 definiert wird hat die
gleiche Diagonale wie das “große” Rechteck, das durch die Strecken a/b definiert wird.
Rechtecke mit gleichen Diagonalen haben auch das gleiche Seitenverhältnis.
Also gilt auch das folgende:
$ a1 = b1 * sqrt(n) $ oder $ b1 = (a1) / sqrt(n) $ - Jetzt folgt der erste wichtige Schritt unseres Beweises. Da die Diagonale und ihre Umkehrung
innerhalb
des Rechtecks ein rechtwinkliges Dreieck erzeugen, können wir die Formel für den
Abstand (die Höhe) des rechten Winkels zur Diagonale benutzen.
$ h^2 = p * q $
Wir haben ein rechtwinkliges Dreieck, das in der linken oberen Ecke beginnt, dann mit der Länge a bis zur rechten oberen Ecke verläuft, dann die Diagonale entlang bis zum Schnittpunkt der Diagonalen mit ihrer Umkehrung und schliesslich die blaue Linie entlang wieder zurück zur linken oberen Ecke. Wenn wir unsere eigenen Variablen in die Höhengleichung einsetzen, erhalten wir folgendes:
$ b2^2 = a1 * a2 $
Um unseren Beweis zu erbringen, sollte unsere Formel nur noch die beiden Variablen a1 und a enthalten, damit wir das Verhältnis zwischen beiden Strecken angeben können. Also ersetzen wir zunächst a2 durch den Ausdruck $ a - a1 $. Unsere Formel lautet dann:
$ b2^2 = a1 * (a-a1) $ - Gehen wir jetzt daran, die Variable b2 loszuwerden. Der erste Schritt besteht darin b2
durch eine Kombination aus b und b1 zu ersetzen. Diese beiden Variablen können wir
später durch Ausdrücke ersetzen, die nur noch a und a1 enthalten (siehe Schritt 6).
Für den Moment nutzen wir die Formel aus Schritt 2:
$ (b - b1)^2 = a1 * (a - a1) $ - In Schritt 1 und Schritt 3 haben wir schon Formeln für b und b1 angegeben,
die nur noch von a, a1 und n abhängig sind.
Wir benutzen sie, um b und b1 zu ersetzen:
$ (a / sqrt(n) - (a1) / sqrt(n))^2 = a1 * (a - a1) $ - Jetzt sind wir schon fast fertig - unsere Formel enthält nur noch die Variablen a,
a1 und n. Wir müssen die Formel nur noch vereinfachen. Beginnen wir mit der linken Seite:
$ (a - a1)^2 / n = a1 * (a - a1) $ - Nun multiplizieren wir mit n:
$ (a - a1)^2 = n * a1 * (a - a1) $ - Auf der rechten Seite stört die Subtraktion. Interessanterweise kann man die gleiche
Subtraktion auch auf der linken Seite finden (quadriert). Also dividieren wir einfach beide
Seiten durch den Subtraktions-Term ( $ a - a1 $ ):
$ a - a1 = n * a1 $ - Jetzt sieht die Formel schon richtig einfach aus. Da wir herausbekommen wollen, wie viele
Teilrechtecke im Wurzel-n-Rechteck enthalten sind, müssen wir das Verhältnis zwischen
a und a1 ermitteln. Also müssen wir dafür sorgen, dass auf der linken Seite der
Gleichung kein a1 mehr zu finden ist. Dazu addieren wir auf beiden Seiten a1:
$ a = n * a1 + a1 $ - Wir wollen nur ein Verhältnis als Ergebnis - also sollte auf der rechten Seite auch nur
einmal die Variable a1 zu sehen sein. Also drücken wir die Addition anders aus:
$ a = (n+1) * a1 $
Und schon haben wir unser Ergebnis: Wir haben bewiesen, dass ein Wurzel-n-Rechteck in n+1 gleich große Rechtecke teilbar ist, wenn man den Kreuzungspunkt der Diagonale mit ihrer Umkehrung als Position für die erste Senkrechte benutzt.
Falls Sie Interesse an Dynamischer Symmetrie gefunden haben, schauen Sie wieder mal rein!