Fotografie Blog

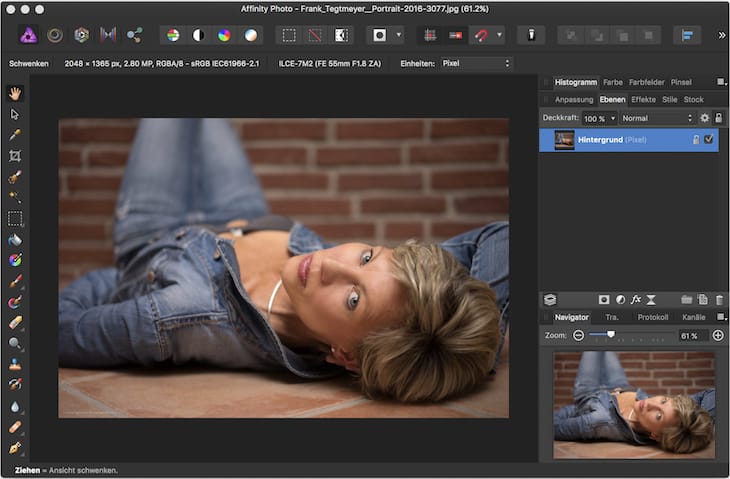
Warum man den Bereich des größten Kontrasts bei der Bildanalyse gebrauchen kann habe ich in einem der letzten Artikel erläutert. Im jetzigen Artikel geht es darum, wie man diese Analyse in Affinity Photo durchführt.

Seit Jahren gestalte ich einen Kalender mit eigenen Aufnahmen, den wir in der Küche aufhängen. Hier die Version dieses Jahres (2017).

Dieser Artikel ist Teil einer Serie, die Bildkomposition unter Nutzung der Dynamischen Symmetrie und der Gestalttheorie behandelt. In diesem Beitrag geht es um den Bereich des größten Kontrasts (englisch: greatest area of contrast oder auch GAC) in einem Bild, der gezielt zur Bildgestaltung eingesetzt werden kann.

Das Goldene Rechteck ist eine der bekanntesten Rechteckformen, da es in enger Beziehung zum Goldenen Schnitt steht. Andere Namen sind Phi-Rechteck oder auch Rechteck der wirbelnden Quadrate. Der Artikel behandelt die Konstruktion des Rechtecks und seine besonderen Eigenschaften.

Dieser Artikel ist Teil einer Serie, die Bildkomposition unter Nutzung der Dynamischen Symmetrie und der Gestalttheorie behandelt. Teilweise werden Kenntnisse aus den anderen Artikeln vorausgesetzt. Am besten ist es, alle Artikel der Serie zu lesen.

Dieser Artikel ist Teil einer Serie, die Bildkomposition unter Nutzung der Dynamischen Symmetrie und der Gestalttheorie behandelt.

In diesem Beitrag stelle ich das Rabatment vor - eine Kompositionsmethode, die nichts mit Dynamischer Symmetrie zu tun hat, aber über die Jahrhunderte sehr oft in Kunstwerken nachzuweisen ist.

Beim Studium der Videos von Myron Barnstone und auch in einigen Artikeln von Tavis Leaf Glover wurden “Themen” von Wurzel-Rechtecken (und auch anderen Spezial-Rechtecken) erwähnt. Ein Thema ist dabei so zu verstehen, dass die Aufteilung des Rechtecks in eine bestimmte Anzahl von Teil-Rechtecken möglich ist bzw. durchgeführt wird.

Speziell zu den Wurzel-Rechtecken gab es die Aussage, dass zu Wurzel-n-Rechtecken (für den Fall dass n eine natürliche Zahl ist) jeweils die Themen n und n+1 gibt. Weil das geometrisch nicht einfach ersichtlich ist, habe ich diese Aussage mathematisch bewiesen.